Monthly Archives: August 2011
سیستمهای پیچیده – بیست و پنج – جای خالی تحقیق در زمینههای علوم
«ارز لیبرمن» میگفت به زمینههای مختلف علوم میتوانیم در مقیاسهای مختلفی نگاه کنیم. چیزی شبیه به طرح پایین:

پیشنهاد میکرد که اگر میخواهید چیزی به مجموعهی دانش اضافه کنید، به دنبال این نباشید که در هرکدام از این زمینهها آخرین پیشرفتها را دنبال کنید و بعد به دستآوردهای قبلی چیزی اضافه کنید. آن چیزی که در حال حاضر خلا و نبودش احساس میشود، فاصلههای خالی بین این زمینهها است. به دنبال این باشید که چه طور این زمینههای مختلف که در مقیاسهای متفاوتی هستند، به هم ارتباط پیدا میکنند. با دید بهتر در این مورد میتوان به دید بهتری در این مورد رسید که چه طور اجزای کوچک با تعامل با یکدیگر، ساختارهایی در مقیاسهای بزرگتر میسازند.
جمعیت این کرهی کوچک
برای دیدن کل مطلب و تعداد زیادی تصویر که به خودی خود گویا هستند، به اصل مقاله مراجعه کنید.
یکی از بازیهای مسخرهی دوران کودکی من
در دوران کودکی (مثلا وقتی که حدودن ده ساله بودم) برای خودم یک بازی (یا یک بیماری) اختراع کرده بودم که به این شکل بود: تصور میکردم که یک طناب به پشت من وصل شده و اون یکی سرش نامحدوده و به جای نامعلومی گره خورده. حالا اگر میخواستم به جایی برم، خیلی احتیاط میکردم که حتمن مسیر برگشتم با مسیر رفت یکی باشه. در غیر این صورت طناب گیر میکرد. مثلن اگر از یک اتاق به اتاق دیگه میرفتم و سر راه یک ستون بود، مهم نبود که از سمت چپ ستون رد بشم یا از سمت راست؛ مهم این بود که حواسم باشه که بعدن از همون سمت ستون برگردم. در غیر این صورت طناب به ستون گیر میکرد. وقتی که سوار ماشین میشدم، حتمن اصرار داشتم که از همون دری پیاده بشم که سوار شده بودم. در غیر این صورت طناب از داخل ماشین رد شده و گیر کرده بود. گاهی مثلن از در سمت راست سوار میشدم و بعد مجبور میشدم از در سمت چپ پیاده بشم. در این مواقع حواسم بود که دفعهی بعدی از در سمت چپ سوار بشم و از در سمت راست پیاده بشم که به این ترتیب طناب از توی ماشین در اومده باشه.
دیشب داشتم بدمینتون بازی میکردم. سرویس دست ما بود و من باید برای شروع به پشت سر همبازیام میرفتم. از این که از سمت چپاش حرکت کردم معذب شدم، چون احساس کردم من قبلن از سمت راستاش اومده بودم. با این ترتیب طناب به دور همبازیام میپیچید و گیر میکرد.
این بازی-بیماری اختراعی من سالها پیش به پایان رسیده بود، چیزی نزدیک به بیست سال پیش. اما عجیب بود که بعد از این مدت زیاد، به طور ناگهانی و بدون مقدمه خودش رو نشون داد. گویا به پایان نرسیده بوده.
نتیجهگیری یک: اگر دیدین که بچهها گاهی کارهای عجیب و غریب میکنن، در نظر بگیرین که شاید دارن بازی میکنن.
نتیجهگیری دو: اگر دیدین که بزرگترها گاهی کارهای عجیب و غریب میکنن، در نظر بگیرین که شاید هنوز از بعضی درگیریهای کودکی رها نشدهاند.
سیستمهای پیچیده – بیست و چهار – چرا موجودات زنده میمیرند، اما شهرها نه
چرا شرکتها و کمپانیها ممکن است بعد از مدتی از بین بروند (بمیرند)، اما چنین اتفاقی برای شهرها نمیافتد؟ آیا شهرها شبیه به جنگل هستند که زندگی میکنند و همچنان در طی سالها و سالها به حیات خود ادامه میهند؟
به نظر «جفری وست» رشد یک موش کمابیش مشابه شکل زیر است
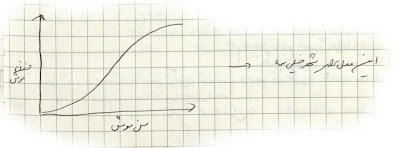
در این مدل خصوصیت مورد نظر بعد از مدتی اشباع میشود که برای شهر مناسب نیست. یک شهر نیاز دارد که به طور پیوسته رشد کند تا به حالت رکود نرسد.

در تصویر بالا شکل بالایی رشد شهر در زمان را نشان میدهد. در این شکل خصوصیت مورد نظر با سرعت زیاد رشد میکند. اما در عین حال رشد به این شکل برای همیشه ممکن نیست. مثلن ممکن است منابع تمام شوند و در نتیجه مجموعه بعد از مدتی فروبپاشد. برای جلوگیری از فروپاشی هر از گاهی نیاز به «نوآوری» داریم. اگر نوآوری داشته باشیم، روند رشد شهر از شکل بالایی به شکل پایینی در تصویر بالا تغییر میکند. به عبارت دیگر هر نوآوری فرصتی دوباره برای رشد بیشتر ایجاد میکند. به عنوان نمونههایی از نوآوری، کشف آهن، اختراع برنز، اختراع کامپیوتر و اختراع تکنولوژی اطلاعات را در نظر بگیرید. در نتیجه با این نوآوریها از فروپاشی مجموعه جلوگیری کردهایم. اما یک مشکل دیگر هم باقی مانده: برای این که با این مدل بتوانید ادامه دهید، لازم است به طور پیوسته فاصلهی بین هر دو نوآوری را کاهش دهید. یعنی سرعت معرفی نوآوریها را پیوسته بیشتر و بیشتر کنید تا مجموعه فرونپاشد.
سیستمهای پیچیده – بیست و سه – شباهت شهرها با موجودات زنده
«جفری وست» معتقد است تمام موجودات زنده، با هر اندازه و در هر مقیاسی که باشند، یک مجموعه خصوصیتهای مشترک دارند. برای نمونه اگر نمودار مصرف انرژی نسبت به جرم موجود را در یک نمودار لگاریتمی رسم کنیم، چیزی شبیه به شکل زیر خواهد بود.
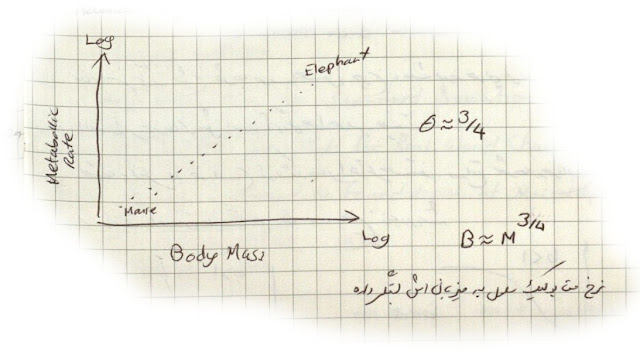
یعنی مهم نیست که موجود زنده یک موش دو گرمی باشد یا یک نهنگ دویست میلیون گرمی. به هر حال این رابطه بین مصرف انرژی و جرم برقرار است. به عبارت دیگر میتوان با دانستن جرم یک موجود، میزان مصرف انرژی آن را تا حد خوبی تخمین زد. شیب خط نزدیک به سه چهارم است. با این ترتیب اگر جرم موجود الف دو برابر موجود ب باشد، مصرف انرژی آن دو برابر نیست؛ بلکه تنها هفتاد و پنج درصد بیشتر است. معنی جالبی در این موضوع هست: موجودات بزرگتر کارایی بهتری دارند و در مصرف انرژی بهینهتر هستند!

مشابه این رابطه در مورد خیلی از دیگر خصوصیتهای موجودات زنده صادق است. برای نمونه تعداد ضربان قلب و میزان خواب هم کمابیش از این قانون پیروی میکنند (هرچند به صورت معکوس، اما همچنان با همان شیب).

اما مساله تنها محدود به موجودات زنده نیست. ظاهرا شهرها هم از قانون مشابهی پیروی میکنند. برای نمونه اگر بعضی خصوصیتهای شهرها را نسبت به جمعیت در یک نمودار لگاریتمی رسم کنیم، شکلی مشابه موجودات زنده خواهیم دید.

به طرز جالبی تعداد جایگاههای بنزین هم به همین ترتیب متناسب با جمعیت شهر هستند. طول جادهها و شبکهی برقکشی و درآمد و تعداد اختراعها هم کمابیش از همین قانون پیروی میکنند. حتا سرعت راه رفتن مردم در شهر هم با همین نسبت زیاد میشود. از طرف دیگر موارد ناخوشایند مثل میزان جرم و جنایت هم تابع همین قانون هستند. بنا به نظر جفری وست، با این ترتیب شهرهای بزرگتر کارایی بهتری دارند چرا که از زیرساختهای قبلا ساخته شده مثل شبکهی برق و جادهها استفادهی بهتری میشود.
جفری وست تازگی یک سخنرانی تد هم داشته اینجا قابل دسترسی است (شاید در پایین ویدیو دیده شود).
پسنوشت: در مورد این موضوع با دو نفر که در زمینهی شهرسازی (یا رشتههای مشابه) مشغول به تحصیل هستند صحبت کردم. به طرز عجیبی هیچ کدام اجازه ندادند به نیمهی صحبتام برسم و بعد از دو دقیقه صحبتهای من را قطع کردند و هر کدام به مدت نیم ساعت در مورد موضوع صحبت کردند. این پسنوشت را اضافه کردم که یادآوری کنم برای شهرسازها، شهر مسالهای ناموسی است. سخت میپذیرند که «دیگران» در مورد شهر صحبت کنند. در صحبتهای خود در این مورد دقت نظر به خرج دهید و یا اگر هم در مورد شهر صحبت میکنید، چنین وانمود کنید که در مورد «شهر» صحبت نمیکنید! (از ما گفتن!)


