برایان معتقده که برخلاف اونچه که اول تصور میشه، وسایل پیشگیری از بارداری، در ارتباط با جنس مخالف، قدرت خانمها رو در مذاکره کاهش داده. میگه که قبلترها خانم از رابطهی جن.سی خودداری میکرده و خطر بچهدار شدن رو یادآوری میکرده. در نتیجه اگر دو نفر ارتباط جن.سی برقرار میکردن، با این تضمین بوده که ازدواج بکنن. اما الان دیگه این برتری رو از دست دادن؛ چرا که آقا میدونه که ارتباط بدون بچهدار شدن هم ممکنه و نیازی به این نیست که از پیش زیر بار ازدواج بره.
Category Archives: دانش
برای کسانی که به دنبال ساختن سریع وبسایت هستن
اگر قصد ساختن وبسایت برای خودتون دارین و نمیخواین که با مسایل هاستینگ و دامنه هم درگیر بشین، یک انتخاب خوب شاید باغهای دروپال باشه. اگر هم قصد ساختن سایتی ویکیگون دارین، شاید ویکیدات انتخاب خوبی باشه.
The purpose of computing is insight, not numbers
Richard Hamming
مدلی برای بازی مافیا
از دردهای امتحان جی آر ای
من از ایران زیاد ایمیل دریافت میکنم که در مورد امتحان جی آر ای (GRE) سوالهایی میپرسن. به تمام کسانی که در این مسیر هستن این رو پیشنهاد میکنم: ممکنه که امتحان مشکلی باشه یا استرس داشته باشه. اما به نظر من نکتهاش همینه. شما در زندگی آکادمیک آیندهتون گرفتاریهایی بزرگتر از امتحان جی آر ای خواهین داشت که کم هم نیستن. در واقع اگر تحصیلات تکمیلی رو به عنوان راه آیندهتون انتخاب کردین و مایل هستین که تحقیق (معادل کلمهی research) کنین، کاملا طبیعیه که استرس داشته باشین، ناامید و دلسرد بشین، تنش داشته باشین، خسته بشین و با هزار و یک مشکل دیگه مواجه بشین که همگی هم محتمل هستن. پس از همین الان به فکر باشین و سعی کنین از همین مراحل لذت ببرین. به نظر من شاید جی آر ای به نوعی داره این رو میسنجه که شما کی کوتاه میآیین و دست میکشین. اگر کوتاه اومدین و ناامید شدین، مسلما باختهاین. تا زمانی که دارین دست و پا میزنین و کلنجار میرین، هنوز زنده هستین و هنوز امید هست.
چه در امتحانهایی مثل جی آر ای و چه در دوران تحقیقتون، باید بتونین خوش بگذرونین و لذت ببرین که بتونین این مسیر رو ادامه بدین. نظر شخصی من اینه که بعد از امتحان جی آر ای الزاما دنیای بیدردسر و راحتی وجود نداره. بعدش وارد مجموعهی جدیدی از گرفتاریها میشین. باز هم دست خودتونه: سخت بگذرونین و تلخ بگذره به امید تموم شدن، یا این که لذت ببرین و همراه باهاش «زندگی بکنین». به نظر من محقق موفق کسیه که با «درد» تحقیقاش «زندگی» میکنه. از من بپذیرین: زندگی مهمترین چیزیه که میتونین دنبال کنین. ازش غافل نشین!
پس نوشت: در این صفحه چند سوال و جواب متداول نوشتهام. در این صفحه و این صفحه هم چند خطی در مورد پذیرش و امتحانهای تافل و جی آر ای نوشتهام.
آیا مشکل از ماست؟
در ویدیوی زیر، یک استاد دانشگاه ییل از آزمایشهایی میگه که انجام دادهان. از یک گونه میمون استفاده میکنن که سی و پنج میلیون سال پیش با ما (یعنی انسانها) ریشهی مشترک داشتهان (یعنی ما و این میمونها یک جد مشترک داشتهایم که سی و پنج میلیون سال پیش زندگی میکرده). این گروه تحقیقاتی از قطعات فلزی گرد استفاده میکنن و به میمونها یاد میدن که این فلز ارزش داره و میمون میتونه در ازای دادن اون فلز، غذا دریافت کنه. به این ترتیب مفهوم پول رو به میمون یاد میدن. متوجه هم میشن که میمون میتونه مفهوم قیمت رو بفهمه: وقتی دو انتخاب داره، انگور ارزونتر رو میخره. بعد یک بازار مالی ساده برای میمونها تشکیل میدن تا ببینن که آیا اشتباهات اقتصادی ما رو میمونها هم مرتکب میشن یا نه.
سخنران این طور نتیجه گیری میکنه که اشتباهات اقتصادی ما الزاما به خاطر نقص بازارها یا محیطهای اقتصادی ما نیستن؛ بلکه ما خودمون از نظر مغزی اشکال داریم که اجازه نمیده همیشه تصمیمهای عاقلانه بگیریم و همین اشکال رو میمونهای فامیل هم دارن. این طور میگه که مثل مشکل ضعف بینایی، این هم یک مشکله که شاید بعدتر بتونیم بهش غلبه کنیم. برای جزییات بیشتر ویدیو رو ببینین (لطفا اگر در توضیحات اشتباهی داشتم، تصحیح کنین).
سیستمهای پیچیده – شانزده – پولدارترین فرد جهان پولدارتر است یا بلندقدترین فرد جهان بلندقدتر؟
مورد یک: در یک اتاق چند نفر نشستهان (مثلا ده نفر). میانگین ثروت این چند نفر یک مقدار مشخصه. حالا پولدارترین انسان کرهی زمین رو به این چند نفر اضافه کنین (مثلا بیل گیتس یا وارن بافت). با اضافه شدن این شخص جدید، میانگین ثروت افراد چه قدر تغییر میکنه؟ مثلا شاید میانگین ثروت افراد در اول پنجاه هزار دلار بوده که با اضافه شدن شخص جدید میانگین به پنج میلیارد دلار میرسه. یعنی میانگین ثروت افراد اتاق صدهزار برابر میشه.

مورد دو: در همون اتاقی که گفته شد، میانگین قد افراد یک مقدار مشخصه (مثلا یک متر و هفتاد سانتیمتر). حالا بلندقدترین انسان کرهی زمین رو به اون جمع اضافه کنین. میانگین قد چه قدر اضافه میشه؟ مثلا اگر ده نفر در اتاق باشن و بلندقدترین انسان قدش دویست و چهل و شش سانتیمتر باشه، میانگین قد افراد جمع به صد و هفتاد و هفت سانتیمتر میرسه. یعنی فقط هفت سانتیمتر بیشتر از صد و هفتاد سانتیمتر میانگین قبل از ورود این شخص!

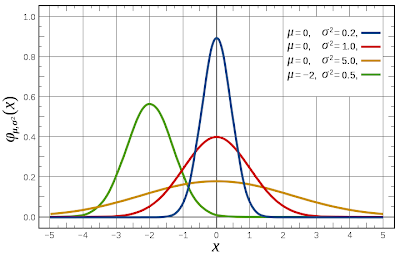
دو مورد بالا مقایسههای خوبی هستن بین توزیعهای نمایی توانی و نرمال. به خاطر محدودیتهای بیولوژیکی یا محدودیتهای دیگه، توزیع قد انسانها نرماله. یعنی همگی حول و حوش یک میانگین هستیم و تعدادی کمتر هستن و تعدادی هم بیشتر. عملا هم قد از یک اندازه بیشتر یا از یک اندازه کمتر نداریم. در مورد وزن هم همینطوره. ولی توزیع ثروت بیشتر از توزیع نمایی توانی پیروی میکنه. در اون مورد این محدودیتها رو نداریم و در نتیجه ثروت بعضیها میتونه خیلی خیلی بیشتر افزایش پیدا کنه.
این متن برداشتی بود از صحبتهای «استیون استروگاتز» در «مجموعهی آموزشی آشوب».
پس نوشت: با تشکر از سولوژن به خاطر یادآوری عبارت درست قانون توانی به جای توزیع نمایی؛ هرچند که مطمئن نیستم که آیا power law رو درست ترجمه کردهام یا نه
تقارن

ساختار بالا که به Montreal Biosphere معروفه، در مونترال کاناداست. از نکات جالبش (که ناگفته پیداست)، تقارنشه. در ضمن اگه درست متوجه شده باشم، در کل این ساختار مثلثها تشکیل ششضلعی میدن به جز دوازده مورد که تشکیل پنجضلعی دادهان. در شکل زیر بعضی از پنجضلعیها معلوم هستن.

منبع اولیهام هم این کتاب بوده
سیستمهای پیچیده – پانزده – چه ماشینی بخریم؟
«جنا بدنار» گفت فرض کنین که در یک شهر ماشینها یا «مینیماینر» هستند یا شاسیبلند. با این ترتیب برای دو ماشین که همدیگه رو در خیابون میبینن، چهار حالت وجود داره: اولی مینیماینر یا شاسیبلند و دومی مینیماینر یا شاسی بلند. اگر هر دو شاسیبلند باشن، به هر کدوم یک امتیاز تعلق میگیره (مثلا با این عنوان که همدیگه رو دیدن و کیف کردن و خطری هم پیش نیومد). اگر هر دو مینیماینر باشن، به هر کدوم دو امتیاز تعلق میگیره (مثلا با این عنوان که هر دو مصرف پایینی دارن و خطری هم تهدیدشون نمیکنه). اگر یکیشون شاسیبلند باشه و اون یکی مینیماینر، به شاسی بلند یک امتیاز تعلق میگیره و به مینیماینر یک امتیاز منفی (علتاش هم اینه که در صورت تصادف خطر بیشتری متوجه مینیماینر میشه در حالی که ماشین شاسیبلند امنیت بیشتری داره). حالا با این ترتیب بگین که اگر یک نفر بخواد ماشین جدید بخره، بهتره که ماشین شاسی بلند بگیره یا مینیماینر؟
برای روشنتر شدن موضوع، مساله رو به شکل یک بازی با ماتریس زیر نشون میدیم:
| SUV | Mini | |
| SUV | 1,1 | 1,-1 |
| Mini | -1,1 | 2,2 |
در ماتریس بالا در هر خونه عدد سمت چپ نشون دهندهی امتیازیه که به ماشین سمت چپاش تعلق میگیره و عدد سمت راست هم امتیازی که به ماشین بالایاش تعلق میگیره. مثلا در خونهی بالا سمت راست، یک امتیاز به ماشین شاسیبلند تعلق میگیره و یک امتیاز از مینیماینر کم میشه.
و اما این که یک نفر چه تصمیمی بگیره، خیلی بستگی داره به این که دیگران قبلا چه تصمیمی گرفتهان. به عبارت دیگه ترکیب ماشینهای موجود در شهر مشخص میکنه که گرفتن چه ماشینی به صرفهتره. مثلا در شهری که اکثر ماشینها مینیماینر هستن، گرفتن ماشین شاسیبلند کمصرفهتره (چون اگر مینیماینر داشته باشیم، تعداد مینیماینرهای بیشتری ملاقات میکنیم و طبق خونهی پایین سمت چپ در جدول بالا، هر بار دو امتیاز میگیریم هرچند که شاید هر از گاهی یک ماشین شاسیبلند ببینیم و یک امتیاز از دست بدیم). از اون طرف اگر ماشین غالب در یک شهر شاسیبلند باشه، داشتن مینیماینر بهصرفه نیست: شانس دیدن شاسیبلند زیاده و هربار یک امتیاز از دست میدیم در حالی که شانس کمی برای دیدن مینیماینر و کسب دو امتیاز داریم.
و اما مرز این تصمیمگیری کجاست؟ حل مساله به شکل عمومی را به خوانندگان علاقهمند و پرشور واگذار میکنیم (یا بهم بگین که در مورد روش حلاش بیشتر توضیح بدم). فقط این رو بگم که به اعداد داخل جدول بالا بستگی داره. برای مثالی که گفته شد، اگر یک سوم ماشینها شاسیبلند باشن و دو سوم بقیه مینیماینر، در اون صورت فرقی نمیکنه که یک نفر ماشین جدیدش رو چی بگیره (چون در هر دو حالت دقیقا یک مقدار سود به دست مییاره). اگر (حتا کمی) بیش از یک سوم ماشینها شاسیبلند باشن، بهتره که یک نفر ماشین جدیدش رو شاسی بلند بخره و به همین ترتیب اگر (حتا کمی) کمتر از یک سوم ماشینها شاسیبلند باشن، بهتره که یک نفر ماشین جدیدش رو مینیماینر بخره که سود بیشتری به دست بیاره.
نظر شخصی: وضعیتای که در بالا گفتم (مثلا یک سوم و دو سوم) یک نقطهی تعادله. یعنی سود و ضرر برای هر دو انتخاب یکسانه. از طرف دیگه این تعادل پایدار نیست. مثلا فرض کنین تعداد ماشینها دقیقا اون چیزیه که گفتم و شما یک ماشین شاسیبلند بخرین. در این صورت تعادل رو به هم زدین و از این به بعد افراد بعد از شما همه به سمت خرید ماشین شاسیبلند میرن (چون دیگه به صرفهتره). در عین حال این پروسه روی دیگران هم تاثیر میگذاره و به همین ترتیب خرید ماشین شاسیبلند بیشتر و بیشتر میشه. این یک نمونه از فیدبک مثبت هست.
مثال عملی: در تگزاس تعداد زیادی از ماشینها بزرگ هستن. یا شاسیبلندن یا وانتبارهای بزرگ یا ون. با این مدل که در بالا گفتم، قابل درکتر میشه که داشتن یک ماشین بزرگ مقداری امنیت بیشتر برای صاحب ماشین به همراه مییاره و مقداری نا امنی برای دیگران. پس دیگران هم مجبور شدن که ماشینهای بزرگتر بگیرن که با این پدیده مقابله کنن و در نتیجه همه در این دور افتادهان چنان که الان تعداد زیادی از آدمها ماشین بزرگ میگیرن که امنیت بیشتری برای خودشون فراهم کنن. شاید در خیلی از ایالتهای دیگه چنین وضعی نباشه و سود داشتن ماشین کوچیک بیشتر باشه.
توضیح اضافه: اگر جدول بالا به هر دلیلی تغییر بکنه، شرایط و رفتار مردم هم تغییر میکنه. مثلا اگر قیمت بنزین بالا بره، سود داشتن ماشین کوچیک بیشتر میشه (عدد خونهی پایین سمت راست) و در نتیجه نقطهی تعادل هم جابهجا میشه.
سیستمهای پیچیده – چهارده – وقتی هشتاد درصد ثروت جامعه در درست بیست درصد افراده

«تام کارتر» از یک مدل ساده برای توزیع ثروت صحبت کرد. فرض کنین در ابتدای کار در جامعه تعدادی آدم داریم (در این مورد چهارصد نفر، که در شکل بالا هر نقطه نشون دهندهی یک نفره) که هرکدوم یک مقدار مشخص پول دارن (مثلا هرکس پنجاه تومن). حالا قانون اینه که دو نفر آدم تصادفی انتخاب کنین و یک تجارت ساده بینشون شکل بدین: اولی یک تومن به دومی میده. این کار رو هم تکرار کنین. حالا حدس بزنین که بعد از یک مدت تکرار چه اتفاقی میافته. آیا همه همچنان ثروتشون کمابیش با هم برابره؟ آیا توزیع ثروت همچنان برابرانه است؟ (شاید نشه گفت که ثروت مساوی بین همهی آدمها الزاما عادلانه است)
.
.
.
.
.
.
.
.
.
.
کمی فکر کنین…
.
.
.
.
.
.
کمی بیشتر فکر کنین…
.
.
.
.
.
.
.
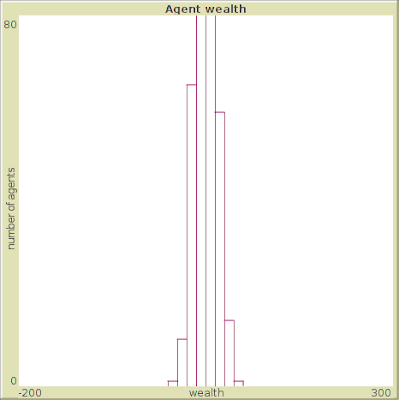
در واقع در اول کار توزیع ثروت به این شکله:

بعد که این قانون رو اعمال میکنیم، توزیع ثروت کمکم عوض میشه. یک قشر پولدار پیدا میشن و یک قشر کمپول. یک قشر متوسط هم هستن که اکثریت رو دارن (گروهی که در وسط هستن):
و بیشتر هم ادامه میدیم و این شکل توزیع ثروت تشدید میشه:
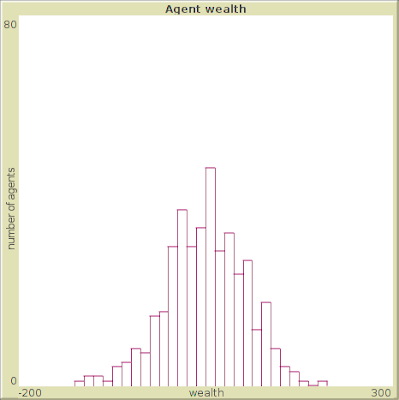
به عبارتی توزیع ثروت از توزیع نرمال (منحنی زنگولهای) پیروی میکنه. یعنی حتا با این قانون ساده (و شاید عادلانهی) مبادلات اقتصادی هم یک گروه پولدارتر میشن و یک گروه فقیرتر. اما در این پروسه ما یک چیز رو در نظر نگرفتیم (که باعث میشه که مدل خیلی دقیق نباشه). در مدل بالا هیچ محدودیتی برای حد پایین ثروت نذاشتیم، به این معنا که ثروت یک نفر میتونه منفی بشه یا به عبارت دیگه بدهکار بشه. در عکس بالا هم یک گروه هستن که ثروت منفی دارن. حالا فرض کنین که این محدودیت رو اعمال کنیم و یا به بیان دیگه به کسانی که پول ندارن، اجازهی خرج کردن پول ندیم. در این حال حدس بزنین که توزیع ثروت بعد از چند مرحله چه طور خواهد بود.
.
.
.
.
.
.
.
.
.
.
.
اول که قبل از شروع تجارتها توزیع به این شکله:

کمی که جلو بریم، توزیع در اوایل شبیه به همون توزیع نرمال هست، چون هنوز همه پول دارن که تجارت کنن. مثل این شکل:
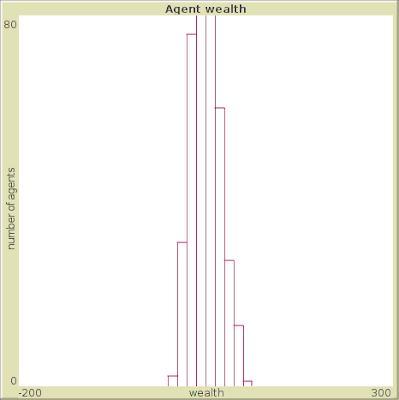
اما با ادامهی مبادلات، کمکم شکل توزیع عوض میشه:
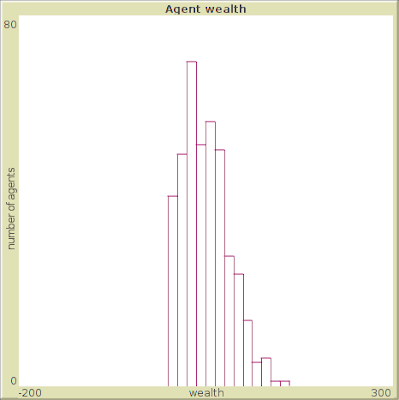
و اگه باز هم ادامه بدیم به این شکل در مییاد:

این توزیع به قانون نمایی معروفه که در سیستمهای پیچیده زیاد دیده میشه. در این توزیع تعداد خیلی کمی ثروت خیلی زیادی دارن و تعداد خیلی زیادی ثروت کمی دارن (به نوعی قانون معروف بیست هشتاد که میگه هشتاد درصد ثروت جامعه در دست بیست درصد افراده). یک نمونهی دیگه این که هشتاد درصد پروازهای دنیا به بیست درصد فرودگاهها انجام میشه. نمونههای خیلی زیادی هست که شاید بعدتر بیشتر در موردشون صحبت کردیم. این قانون به قدری در سیستمهای پیچیده زیاد دیده میشه که گاهی به نوعی شوخی در این جامعه تبدیل میشه.
اگر دوست دارین که با این قانون ثروت کمی بازی کنین، پیشنهاد میکنم به این صفحه سر بزنین و از برنامه استفاده کنین.

