«یانیر باریام» معتقد بود که مثال پاروزنان ریچارد داکینز نقص دارد و یک موضوع مهم را در نظر نمی‌گیرد: موقعیت جغرافیایی. گفت فرض کنید وقتی که قایق‌ران‌ها مسابقه را به پایان می‌رسانند و به جمع مسابقه‌دهنده‌ها برمی‌گردند، به جای این که با بقیه مخلوط شوند، به انتهای یک صف وارد شوند. وقتی هم که قایق‌ران‌ها می‌خواهند مسابقه‌ی جدیدی شروع کنند، افراد تیم‌ها را دو نفر دو نفر از سر صف جدا کنیم و سوار قایق کنیم. در این وضعیت چه اتفاقی می‌افتد؟ آیا استفاده از صف به جای یک گروه درهم، تغییری در نتیجه ایجاد می‌کند؟

اگر کسی در صف همسایه‌های هم‌زبان خودش داشته باشد، شانس پیروزی‌اش بیش‌تر است و اگر همسایه‌ها متفاوت باشند، شانس شکست خوردن‌اش بیش‌تر می‌شود. دو همسایه‌ی غیرهم‌زبان کارایی کم‌تری دارند و در نتیجه به احتمال زیاد از جمع حذف می‌شوند.

با این ترتیب، بعد از مدتی در صف الگو (pattern) شکل می‌گیرد؛ گروه‌های همسایگی از پاروزنان هم‌زبانی تشکیل شده‌اند که نزدیک به هم هستند (که در اصطلاح به آن‌ها مجموعه‌ای از patch ها می‌گویند). درباره‌ی نمونه‌ای از شکل‌گیری الگو در دو پست قبل نوشتم. شکل زیر به نوعی نشان‌دهنده‌ی یک صف است که در آن الگوها شکل گرفته‌اند.

شکل زیر به نوعی نشان می‌دهد که با در نظر گرفتن موقعیت جغرافیایی، چه طور فضا تقسیم می‌شود و گروه‌هایی با اعضایی که رفتار (یا خصوصیت) مشابه دارند کنار هم شکل می‌گیرند. برای مثال در شکل زیر گروه‌های همسایگی از افراد مشابه تشکیل شده‌اند و در نتیجه در قلم‌روی خودشان توانایی زیستی (fitness) بالاتری دارند.

با این ترتیب وقتی جغرافیا را در نظر می‌گیریم، احتمال بیش‌تری برای شکل‌گیری گوناگونی (diversity) هست. اگر همه با هم مخلوط می‌شدند، بسیاری از بین می‌رفتند و تنها یک گروه باقی می‌ماندند؛ اما حالا که هر یک از گونه‌ها فرصت دارد برای خودش قلم‌رو داشته باشد و با افراد مناسب خودش تعامل داشته باشد، در آن محدوده شانس بیش‌تری برای بقا دارد.

از قرار معلوم یانیر باریام با ریچارد داکینز تلفنی در این مورد صحبت کرده، هرچند که سندی مبنی بر قانع شدن داکینز در دست‌رس نیست.

 یک مسابقه‌ی پاروزنی برپاست. در هر قایق دو نفر پارو می‌زنند و هر نوبت دو قایق با هم مسابقه می‌دهند. در شروع هر مسابقه، چهار نفر را به تصادف از جمع پاروزنان انتخاب می‌کنیم و در دو قایق می‌نشانیم. بازندگان از مسابقه خارج می‌شوند و برندگان دوباره به جمع برمی‌گردند، مثل شکل زیر.

شرکت‌کننده‌ها یا انگلیسی‌زبان هستند و یا آلمانی زبان (در شکل بالا با ضرب‌در و دایره نشان داده شده‌اند). اگر دو پاروزن هم‌زبان باشند، به‌تر با هم هماهنگ می‌شوند و کارایی به‌تری دارند. در نتیجه در شکل بالا به احتمال زیاد قایق بالایی برنده خواهد شد، چون پاروزن‌هایش هم‌زبان هستند.

هرچه‌قدر تعداد انگلیسی‌زبان‌ها بیش‌تر باشد، شانس برنده شدن‌شان هم بیش‌تر است؛ هر بار که به تصادف دو نفر را انتخاب می‌کنیم، احتمال بیش‌تری هست که هر دو نفر انگلیسی‌زبان باشند و به همین ترتیب موفقیت کل انگلیسی‌زبان‌ها ادامه پیدا می‌کند. همین مساله در مورد آلمانی‌زبان‌ها هم درست است.

در این سیستم سه نقطه‌ی تعادل داریم.

یکی از تعادل‌ها این است که تعداد انگلیسی‌زبان‌ها و آلمانی‌زبان‌ها دقیقن برابر باشد و به همین ترتیب برابر هم بماند. این تعادل ناپایدار است (در سیستم‌های دینامیکی به آن unstable fixed point گفته می‌شود). وقتی دو نفر را به تصادف انتخاب می‌کنید، به احتمال بیست و پنج درصد هر دو آلمانی‌زبان هستند، به احتمال بیست و پنج درصد هردو انگلیسی‌زبان و به احتمال پنجاه درصد هم یکی آلمانی‌زبان است و دیگری انگلیسی‌زبان. اما کافی است که تعادل کمی جابه‌جا شود و تعداد یک گروه کمی بیش‌تر از گروه دیگر شود. در نتیجه در انتخاب‌های بعدی گروه با تعداد بیش‌تر شانس بیش‌تری برای برنده شدن دارند و به همین ترتیب تعدادشان بیش‌تر و بیش‌تر می‌شود (و همان‌طور که دیدید تعادل از اول هم پایدار نبود).

دو نقطه‌ی تعادل دیگر هم داریم: به تدریج همه‌ی جمعیت هم‌زبان شوند، چه همه‌ی آلمانی‌زبان‌ها باقی بمانند، چه همه‌ی انگلیسی‌زبان‌ها. فرض کنید همه انگلیسی‌زبان هستند. در این شرایط اگر یک آلمانی‌زبان به جمع اضافه شود، شانسی برای بقا ندارد چرا که حتمن موقع مسابقه با یک انگلیسی‌زبان در قایق خواهد بود و در رقابت با یک قایق که هر دو انگلیسی‌زبان هستند، شکست خواهند خورد. در شکل زیر به طور کیفی می‌بینید که این سه نقطه‌ی تعادل کجا هستند. وسط که ناپایدار است و بالا و پایین (معادل صفر و یک) پایدار هستند. برای مثال در شکل پایین عدد می‌تواند نشان دهد که چه کسری از پاروزن‌ها آلمانی هستند (یا انگلیسی)، محور افقی زمان است و هر خط نشان‌دهنده‌ی تغییرات ترکیب جمعیت در زمان است.

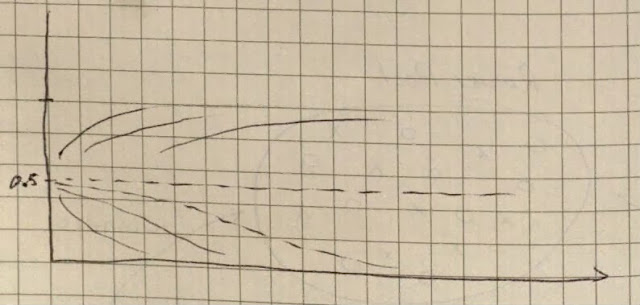در این مثال فرض کنید «انگلیسی‌زبان بودن» یک ژن است و «آلمانی‌زبان بودن» هم یک ژن. قایق هم به نوعی نماد ارگانیسمی است که دربرگیرنده‌ی ژن‌هاست. وقتی یک قایق در مسابقه پیروز می‌شود، به نوعی ارگانیسم موفق بوده، بقا پیدا کرده و ژن‌هایش فرصت گسترش بیش‌تر پیدا کرده‌اند. بنا بر این مثال، ژن‌ها به تنهایی نه بد هستند و نه خوب. به نوعی این محیط است که تعیین می‌کند چه ژن‌هایی شانس بیش‌تری برای بقا دارند و چه ژن‌هایی حذف می‌شوند.

این مثال تنها برای باز کردن موضوع بود و دقیق نیست. برای نمونه در مورد افزایش جمعیت جمع پاروزنان صحبتی نشد؛ می‌توانیم فرض کنیم که هر بار برنده‌ها به جمع پاروزنان برمی‌گردند، تعدادشان دو برابر می‌شود. این مثال در کتاب «ژن خودخواه» نوشته‌ی «ریچارد داکینز» نوشته شده بود. در پست بعدی درباره‌ی اشکالی می‌نویسم که بر همین مثال وارد شده.

فرض کنید یک گروه بچه در یک مهدکودک دورتادور یک میز گرد نشسته‌اند. بچه‌ها اجازه دارند از دو اسباب‌بازی موجود، ماشین و عروسک، تنها یکی را انتخاب کنند و با آن بازی کنند. بچه‌ها ترجیحی برای اسباب‌بازی‌ها ندارند، به جز این که دوست دارند بتوانند با همسایه‌های‌شان بازی کنند. هر بچه تنها دو همسایه، یکی در سمت چپ و یکی در سمت راستش دارد و علاوه بر خودش، تنها به آن دو نفر توجه می‌کند. اگر همسایه‌ها عروسک دارند، بچه هم عروسک را ترجیح می‌دهد و اگر همسایه‌ها ماشین دارند، ماشین گزینه‌ی به‌تری است.

از بچه‌ها می‌پرسیم که چه اسباب‌بازی‌ای دوست دارند و هرکدام یک چیز انتخاب می‌کند. به همه فرصت می‌دهیم که با توجه به انتخاب همسایه‌ها، ببینند اکثریت گروه سه نفره‌ی هرکدام چه چیزی انتخاب کرده‌اند. فرصت تغییر تصمیم می‌دهیم که اگر خواستند اسباب‌بازی‌ها را عوض کنند. وقتی اسباب‌بازی‌ها را عوض کردند، باز هم فرصت می‌دهیم به همسایه‌ها نگاه کنند و اگر خواستند، تصمیم‌شان را عوض کنند؛ به همین ترتیب ادامه می‌دهیم.

با تکرار این الگوریتم، چه الگویی شکل می‌گیرد؟

طبیعتن به شرایط اولیه (initial conditions) بستگی دارد؛ یعنی بستگی دارد که بار اول بچه‌ها چه اسباب‌بازی‌هایی انتخاب کرده باشند و تغییرات بعد از آن بستگی به انتخاب اول دارد. در شکل‌های زیر فرض کنید دایره‌ی توپر نشان‌دهنده‌ی یک اسباب‌بازی باشد و دایره‌ی توخالی نشان‌دهنده‌ی اسباب‌بازی دیگر. در ضمن به جای نشان دادن انتخاب‌ها (بچه‌ها) در یک دایره (به جای میزی که گرد است)، از یک خط استفاده کرده‌ام؛ فرض کنید دو انتهای خط با هم همسایه هستند. هر سطر هم یک مرحله تصمیم‌گیری را نشان می‌دهد.

ممکن است بعد از تصمیم اول هیچ تغییری صورت نگیرد و همه ترجیح بدهند سر تصمیم اول بایستند. مثل چهار بچه‌ی شکل زیر:

●○○●
●○○●
●○○●
●○○●

هر چه قدر هم که تکرار کنیم و به بچه‌ها فرصت عوض کردن اسباب‌بازی بدهیم، این الگو تغییر نمی‌کند. گاهی ممکن است بعد از چند مرحله، همه با هم به یک نتیجه برسند و یکی از دو اسباب‌بازی را اسباب‌بازی انتخاب کنند. مثل بچه‌های شکل زیر:

●●○●○●○●
●●●○●○●●
●●●●●●●●
●●●●●●●●
●●●●●●●●

 به وضعیت بالا در سیستم‌های دینامیکی نقطه ثابت (fixed point) می‌گویند. ممکن است بچه‌ها در هر مرحله تصمیم‌شان را عوض کنند و هیچ وقت هم به نتیجه نرسند. به چهار بچه‌ی زیر نگاه کنید:

●○●○
○●○●
●○●○
○●○●

به وضعیت بالا در سیستم‌های دینامیکی نوسان (oscillation یا گاهی cycle، با توجه به نوع دینامیک) می‌گویند. یک حالت دیگر (که جالب هم هست) شکل‌گیری الگو است. برای مثال بعضی گروه‌ها با ماشین بازی کنند و بعضی با عروسک و این گروه‌ها در کنار هم بمانند و ادامه دهند. برای مثال به شکل زیر توجه کنید:

○●●○○●○○●○●○●●○○●○○○
○●●○○○○○○●○●●●○○○○○○
○●●○○○○○○○●●●●○○○○○○
○●●○○○○○○○●●●●○○○○○○
○●●○○○○○○○●●●●○○○○○○

 در وضعیت بالا چهار گروه مختلف همسایگی شکل گرفته. بعضی‌ها نظرشان را عوض کردند و روی انتخاب جدید ماندند. یک نفر هم نزدیک به وسط انتخابش را عوض کرد و در مرحله‌ی بعد باز هم عوض کرد و به انتخاب اول برگشت و ثابت شد. در شکل بالا دو گروه همسایه با عروسک بازی می‌کنند و دو گروه همسایه با ماشین.

قانون این مهدکودک (که هرکس به اکثریت خودش و همسایه‌ها توجه کند و تصمیمش را عوض کند) قانون به نسبت ساده‌ای بود. اگر قانون پیچیده‌تر باشد، شاید الگوهای پیچیده‌تری هم ظاهر شوند. اگر به موضوع علاقه دارید، در مورد اتوماتای سلولی (cellular automaton) مطالعه کنید. در دو پست آینده می‌نویسم که شکل‌گیری الگو چه طور در فرگشت (تکامل) موثر است و باعث تنوع گونه‌ها می‌شود.